|
Different uses for voting
need different types of voting. |
 |
STV Tally, Game One
|
 |
|
Here is an analogy: Each candidate puts out a box. A voter puts his ballot in his favorite candidate's box. The ballots are counted. If the box gets a quota of ballots, it wins. If not, the voter moves his ballot to another candidate's box. Or, he waits, hoping others will move their ballots to his favorite box. To break that deadlock, we have a rule: If a round of counting ballots finds no winner, the box with the fewest votes is eliminated. Its ballots go to each voter's next (2nd) choice — probably a candidate with similar views and more popularity. If a candidate gets more than enough votes, she wins and a share of her extra votes goes to each supporter's next choice. So even the excess votes are not wasted. Below you can see a whole STV tally turning ballots into reps; 12 ballots add up to 1 rep. The Simple Quota here is:
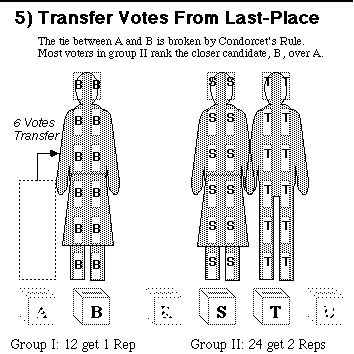
Neighboring candidates have similar opinions so most voters rank them close together. But the 2 interest groups are far apart. Their political positions jump from B to R. STV Protects Majority Rights: The old plurality rule elects A, B, and S. So group I gets 2 reps for 12 voters while group II gets only 1 rep for 24 voters. That is not fair and it does not lead to majority policies. But group I gets no representation if group II gives 2 votes to R, 7 to S, 8 to T, and 7 to U. Plurality rules are erratic as well as unfair. This shows the importance of ranking candidates and transferring votes. To play this game, click whichever group of ballots must transfer. When you click correctly you will jump to the next step of the tally. First look for a candidate with more than enough votes (12) and click on the excess votes. When no one has an excess, click on the smallest stack of ballots. (If you don't like to play, just scroll down to the next step.) |
 |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Here's a hint: look for the candidate with the fewest ballots.
Back to chart 1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
 |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Here's a hint: look for the candidate with the fewest ballots.
Back to chart 2.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
 |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Here's a hint: look for the candidate with excess ballots.
Back to chart 3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
 |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Here's a hint: Candidates A and B each have 6 first-place votes.
You could break this tie with Condorcet's rule.
Would voters in group 2 prefer A or B?
Back to chart 4.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
You made it! Way to go.
|
This page graphically shows how an STV tally works
to protect the majority's right to a majority of seats. The next page shows how STV protects minority rights. 
|

|
|

 Accurate Democracy
Accurate Democracy 








